
Introduction
The AI Tetris Agent essentially is a computer program that plays the game Tetris without any human aid. The goal of the program is to simply clear as many lines as possible - in this case, the agent clears 5 million lines per game on average.
Usage
AI Tetris Agent is available for the Linux, Windows, and Mac OS operating systems.
- Ensure you have Java installed in your computer
- Ensure that you have Java Development Kit (JDK) installed on your computer
- Clone the git repository from here
- Run the following command in the terminal:
javac PlayerSkeleton.java - Followed by this:
java PlayerSkeleton
The agent in progress:

Understanding the Problem
The rules of the game are fairly straightforward. A piece slowly descends from the top and the player is supposed to tactically place it in a position such that it aligns perfectly with the other resting pieces - block of lines or a singular line disappears every time this happens and points are earned. The player is allowed to rotate the falling pieces to his liking before proceeding to place it.
[Picture credits]
For an AI to perform this task similarly - and well - it has to firstly know in which orientation it should place the piece and precisely in which column its final destination should be. Neither the human or the AI could look into the future to determine what the next piece will be. One can only decide on what to do with the current piece at the moment it appears. As long as this is done well, the game could be beaten with a very high score (in the range of millions).
However, it is difficult to define what it means to play a good move. Humans are able to intuitively know if the current state of the game conveys great potential for a long game, whereas it is difficult for the same human to explicitly program this knowledge to define a good move.
Heuristics
This brings forth a need for heuristics. Heuristics of a game state (the game at a particular point in time) are basically insights/estimations that could be used to determine if the current state of the game would lead to a high score.
These were some of the heuristics used in building the agent:
- Number of Holes - Number of rows having at least one hole
- Holes Depth - Number of full cells in the column above each hole
- Cumulative Wells - Sum of the depth of the wells (differs from holes)
- Cell Transitions - The number of empty cells/borders touching the edges of full cells
- Eroded Piece Cells
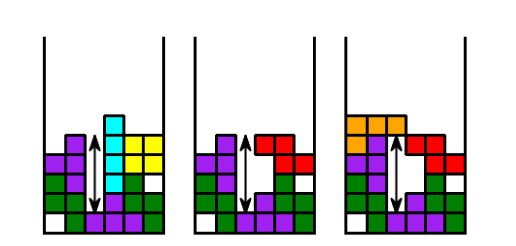
[Wells and Holes - Picture credits]
The idea is that once the agent learns what the next piece is, it runs simulations for all possible moves - orientation and position - using the incoming piece. After simulating each move, it uses the heuristics on the new game state to decide on the most rewarding move among all possible moves. This way, it will have enough time to rotate and place it before time runs out. Doing so sequentially for every single new piece would guarantee a good score in the long run.
However, the problem is to decide on how much weightage should each heuristic get. The agent technically could use a single heuristic instead of multitude of the aforementioned ones. However, this usually does not yield the best results, resulting in the need for multiple heuristics. The root problem, however, is finding the best relative weights for the heuristics.
The problem of beating Tetris using AI essentially translates to an optimization problem - finding the right weights for the heuristics.
Optimization Problem
An optimization problem calls for an optimization algorithm. There are many such algorithms available to solve this problem. A few to name are Artificial Bee Colony (ABC) algorithm, Genetic algorithm, and Particle Swarm Optimization algorithm.
This was a project done with 4 other students in an AI class. Therefore, there was a need to research about the feasibility of different algorithms. A fellow student and I delved into an algorithm called Cuckoo’s Algorithm while the rest worked on others. Eventually we went ahead with ABC algorithm since it was shorter and easier to explain. However, the following paragraphs will explain the Cuckoo’s algorithm since it performed similarly to the ABC algorithm and also since my partner and I worked extensively on it.
The Solution: Cuckoo’s Algorithm

[Picture credits]
The paper describing this algorithm could be found here.
Cuckoos usually lay eggs in other bird’s nests to increase survival and productivity of its own. They do this by imitating the color and pattern of host eggs. Cuckoo’s eggs will hatch earlier than host’s eggs, allowing cuckoo chick/s to evict all other eggs in nest to increase food share.
The algorithm follows a similar strategy:
Each nest represents a solution - normalized weights for each heuristic - and the number of nests are first initialized to 15. Originally all the nests are initialized randomly, however, each of the solution’s potential is gauged by running simulations and observing highscores.
After an iteration, a percentage (20-30%) of the nests are randomly discarded. To pad the removed solutions, new solutions are generated by using the remaining solutions and doing Levy walks with them.
This process is repeated till a good enough solution emerges.
This algorithm eventually - after running for 7/8 hours or so - yielded a solution that gave a reputable highscore.
Tech Stack
This desktop application was built using the following technologies:
- Java Development Kit - Tool used to develop Java applications for the desktop.
Click here to view the code repository.
Thoughts
I was very thankful for this module and project, because it ignited in me an interest for Artificial Intelligence. Any system that tries to find and learn optimum solutions for a problem is always so so interesting to me. We humans draw strict lines for an AI system to follow, and yet, it yields great results in the end.
These are not true intelligent machines of course. But it magically gives a glimpse into the future - systems with true intelligence. And this project pretty much solidified my desire to be part of that future - to be part of the group that will bring that era in.